数据结构(六) 迪杰斯特拉算法的最短路径（Swift面向对象版）

上篇博客我们详细的介绍了两种经典的最小生成树的算法，本篇博客我们就来详细的讲一下最短路径的经典算法----迪杰斯特拉算法。首先我们先聊一下什么是最短路径，这个还是比较好理解的。比如我要从北京到济南，而从北京到济南有好多条道路，那么最短的那一条就是北京到济南的最短路径，也是我们今天要求的最短路径。

因为最短路径是基于有向图来计算的，所以我们还是使用上几篇关于图的博客中使用的示例。不过我们今天博客中用到的图是有向图，所以我们要讲上篇博客的无向图进行改造，改成有向图，然后在有向图的基础上给出最小生成树的解决方案。本篇博客我们的思路与之前数据结构相关博客的风格保持一致，首先我们先给出迪杰斯特拉算法的原理以及详细的示意图，然后根据这些示意图给出具体的实现方案。

 

一、迪杰斯特拉算法原理解析

在博客的第一部分，我们不谈任何与代码相关的内容，只谈迪杰斯特拉算法的原理以及生成最短路径的具体步骤。下方我们会给出迪杰斯特拉算法的计算最短路径的每一步，并给出每一步具体的说明。废话少说，进入本部分的主题。

 

1、有向带权图

本篇博客依然采取我们之前用的图的结构。不过我们本篇博客使用的是有向图。下方这张图就是是我们之前使用的无向图转换过来的，只是给之前的图的边添加的具体的方向，其他的并为改动。由无向图转换后的有向图如下所示，我们将在下方的图的基础上计算出从A到D的最短路径。

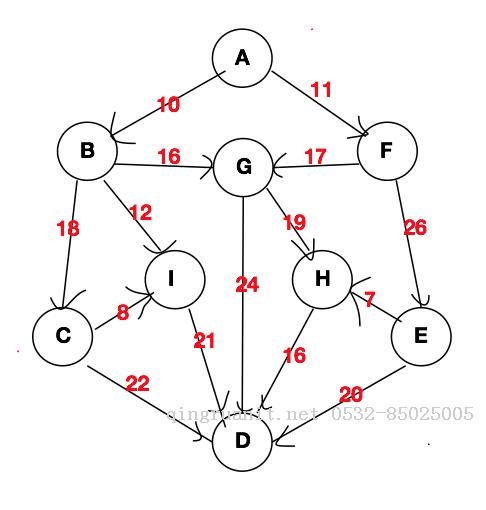
2.迪杰斯特拉算法的具体步骤

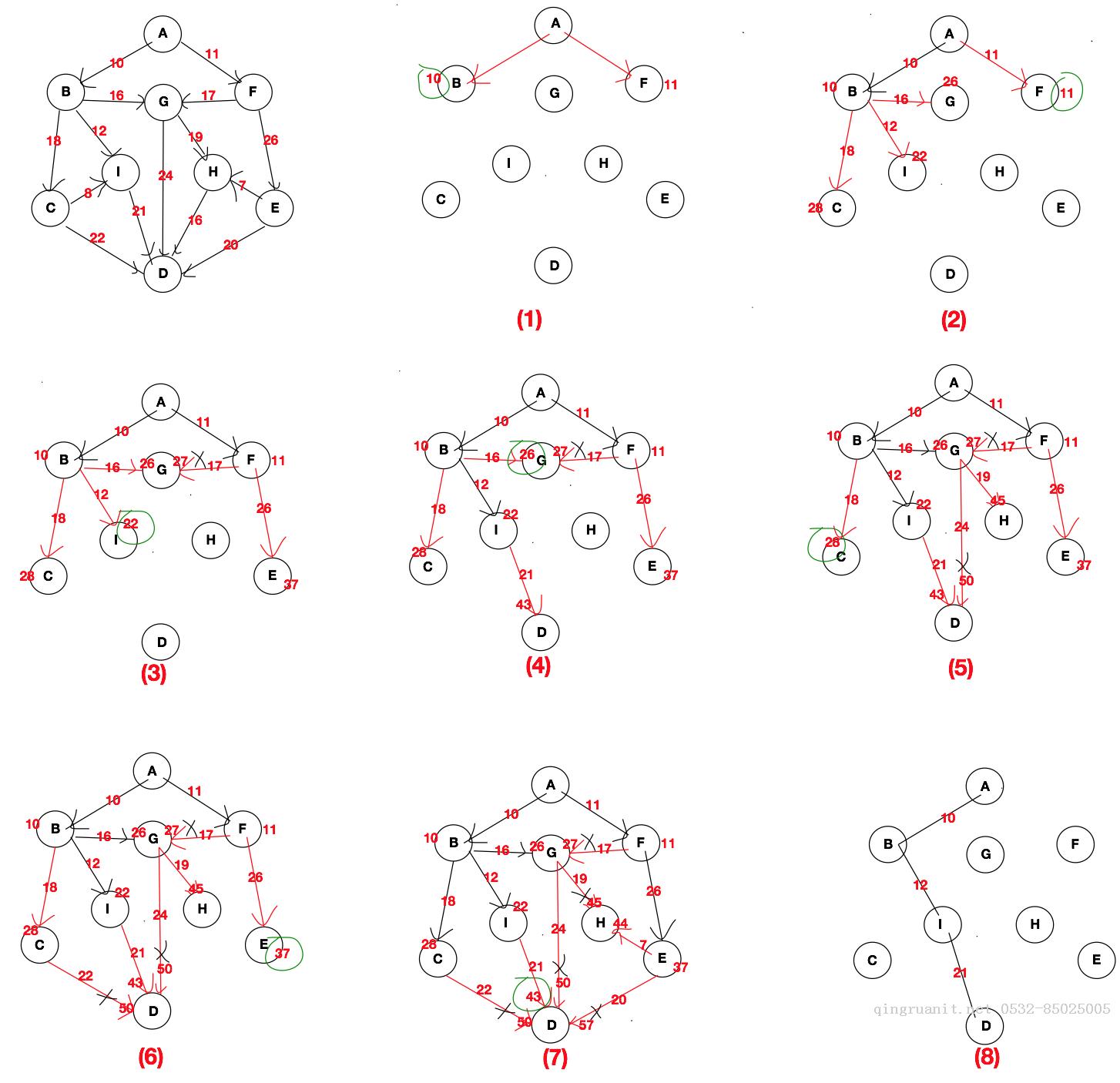
下图就是求上图中A->D的最短路径时使用迪杰斯特拉算法的具体步骤。迪杰斯特拉算法主要核心思想是由起始结点开始，慢慢的由尾结点扩散。直到扩展到尾结点位置。下方我们将根据每个步骤给出具体的介绍：